III. Вращение твердого тела. Основное уравнение динамики вращательного движения. Момент инерции.
Основной закон динамики вращательного движения можно получить теоретическим путем, используя основной закон динамики поступательного движения. Ведь любое вращающееся твердое тело можно представить себе состоящим из множества частичек и к каждой из них применить второй закон Ньютона. Но мы получим основной закон динамики вращательного движения опытным путем. Для установления основного закона динамики вращательного движения может быть использована установка, изображенная на рисунке 1. Металлический диск укреплен на вертикальной оси с помощью шарикоподшипника, что позволяет пренебречь силами трения, возникающими при вращении диска. Измерение угловой скорости производят с помощью центробежного тахометра. Диск приводят во вращение с помощью намотанной на шкив нити. Для этого нить перебрасывают через блок и подвешивают к ее концу груз. Перемещение груза вниз под действием силы тяжести и приводит диск во вращение. В рассмотренном опыте начальная угловая скорость равна нулю (
), поэтому ее значение 
в любой момент времени t определится выражением 
. Измерив время падения груза t и максимальную угловую скорость , которую приобретает диск за это время, можно определить угловое ускорение по формуле 
. Первоначально исследуем зависимость углового ускорения вращения диска от действующей силы 
, если плечо силы относительно данной оси вращения 
остается постоянным (
). Опыт показывает, что при увеличении силы в 2,3,4 и т. д. раз угловаое ускорение увеличивается соответственно во столько же раз. Следовательно, угловое ускорение вращающегося тела прямо пропорционально модулю действующей силы при постоянном плече этой силы: 
~. Затем установим зависимость углового ускорения вращения тела от плеча силы относительно данной оси вращения при постоянной действующей силе (
. Под диском на установке установлены шкивы разного радиуса. Намотав нить на другой шкив (в два раза большого радиуса), можно увидеть, что увеличение плеча силы в два раза при постоянной силе приводит к увеличению углового ускорения диска тоже в два раза. Итак, угловое ускорение вращающегося тела при постоянной по модулю силе прямо пропорционально плечу силы относительно оси вращения: ~, если 
. Так как угловое ускорение прямо пропорционально силе при постоянном значении плеча силы и плечу силы относительно данной оси вращения при постоянном значении силы , то, очевидно, что оно пропорционально их произведению, т. е пропорционально моменту силы 
: ~
. Если намотать нити на два шкива и к ним подвесить грузы, то на диск будут действовать два момента внешних сил. Опыт показывает, что угловое ускорение диска прямо пропорционально сумме всех моментов всех сил, действующих на тело относительно данной оси вращения:~
. Ускорение поступательно движущегося тела зависит от массы тела. Естественно предположить, что и угловое ускорение зависит от массы вращающегося тела. Увеличим массу вращающегося тела. Для этого поставим на диск две гири. При том же моменте действующей силы угловое ускорение вращения диска теперь оказывается меньшим, чем было раньше. Изменим расположение гирь относительно оси вращения диска: отодвинем гири к краям диска. Угловое ускорение при этом еще сильнее уменьшится. Следовательно, угловое ускорение зависит не только от массы вращающегося тела, но и от ее расположения относительно оси вращения. Характеристика тела, зависящая от массы и от ее расположения относительно оси вращения называется моментом инерции (
). Результаты выполненных экспериментов можно записать в виде: 
.
Это основное уравнение динамики вращательного движения: угловое ускорение вращающегося тела прямо пропорционально сумме моментов всех действующих на него сил относительно оси вращения тела и обратно пропорционально моменту инерции тела относительно этой оси вращения. Полученное уравнение аналогично форме записи выражения второго закона Ньютона для поступательного движения тела.
Момент инерции тела сравнительно простой формы может быть определен путем вычислений. Рассмотрим простейший случай – вращение тела по окружности в случае, когда размеры тела пренебрежимо малы по сравнению с радиусом окружности (тело – материальная точка). Если тело закреплено на расстоянии
от от неподвижной оси, то под действием силы 
, направленной по касательной к окружности и перпендикулярно оси вращения, оно приобретает тангенциальное ускорение 
, так как за очень малый промежуток времени 
движение тела по окружности тела можно считать прямолинейным. С другой стороны, рассматривая движение тела как вращательное, угловое ускорение его движения можно определить из основного уравнения динамики вращательного движения: . Из этих двух уравнений получаем выражение для момента инерции тела: 
. Выражая тангенциальное ускорение через угловое ускорение и радиус вращения 
, получаем 
. Итак, момент инерции тела, вращающегося по окружности радиуса , большого по сравнению с размерами тела, равен произведению массы тела на квадрат расстояния от него до оси вращения. Единицы момента инерции в системе СИ: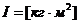 
. Полученный результат позволяет решить задачу о нахождении момента инерции у тел произвольной формы относительно любой оси вращения. Для этого необходимо мысленно разбить это тело на очень маленькие части, найти произведения массы каждой части на квадрат расстояния до оси вращения и все эти произведения сложить.
