Основные кинематические величины

Радиус-вектор – это вектор, который соединяет начало координат с положением тела в пространстве.

Траектория – это кривая линия по которой движется тело.

Перемещение – это вектор, который соединяет начальное и конечное положение тела на траектории.

Путь – скалярная величина, которая равна длине траектории.

Скорость – это физическая величина, которая показывает насколько быстро движется тело. Бывает: а) мгновенная, б) средняя по пути, в) средняя по перемещению.

Ускорение – это векторная физическая величина, которая характеризует быстроту изменения скорости. Бывает: а) нормальное (центростремительное), б) тангенсальное, в) полное.

Тангенсальное ускорение характеризует быстроту изменения скорости по величине.

Нормальное ускорение характеризует быстроту изменения скорости по направлению.

Полное ускорение – это сумма тангенсальной и нормальной составляющих.

2) Основные законы сохранения в динамике пост и вращ движения.

Поступательное движение – это движение тела, при котором прямая, соединяющая любые 2 точки этого тела при перемещении остаётся параллельно своему первоначальному направлению.

Вращательное движение вокруг оси — движение твёрдого тела, при котором какие-нибудь две его точки А. и В остаются всё время неподвижными.

Закон сохранения импульса - импульс замкнутой системы сохраняется.

Закон сохранения энергии - в системе тел, между которыми действуют только консервативные силы, полная механическая энергия сохраняется.

3) Динамика поступательного движения. Законы Ньютона.

Динамика поступательного движения – скорость изменения импульса системы равна главному вектору всех внешних сил, действующих на эту систему.

Основное уравнение динамики поступательного движения:

Инерциальной системой отсчёта является такая система, которая либо покоится, либо движется равномерно и прямолинейно относительно какой-то другой инерциальной системы.

Первый закон Ньютона:

Тело находится в состоянии покоя или равномерного и прямолинейного движения пока воздействие со стороны других тел не заставит изменить его это состояние.

Второй закон Ньютона:

Ускорение, приобретаемое телом пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе тела (dP = Fdt).Для системы материальных точек: dP = ∑(от k = 1 до N)Fk*dt

Третий закон Ньютона:

Все реальные силы в природе являются силами взаимодействия между двумя телами: если 1 действует на тело 2 с силой F12, то тело 2 действует на тело 1 с силой F21(F12=-F21).Т. е. силы с которыми 2 тела взаимодействуют друг с другом равны по модулю но противоположны по направлению (F12 + F21 = 0).

Для системы из N взаимодействий между собой тел 3 закон Ньютона выглядит так:

F12+F21+F13+F31+…= ∑(от i=1 до N)∑(от j=1 до N)Fij =0.

Закон сохранения импульса - импульс замкнутой системы сохраняется(Р=const).

Скорость изменения импульса системы материальных точек равен векторной сумме внешних сил действующих на систему (dP=∑(от k=1 до N)Fk*dt). Это выражение отражает так же и закон сохранения импульса для незамкнутой системы: импульс системы могут изменить только импульсы внешних сил. Если система замкнутая, то:

∑(от k = 1 до N)Fk*dt=0 => dP=0, т. е. импульс замкнутой системы P = ∑(от i = 1 до n)Pi=const.

Моментом импульса материальной точки I относительно начала координат называется векторная величина, которая равна: I = τP

Моментом импульса системы материальных точек L относительно начала координат называется векторная сумма моментов частиц систем.

dL/dt = 0, L=∑(от i = 1 до n)Ii=const – закон сохранения момента импульса для заданной системы.

4) Основное уравнение динамики вращательного движения: M=J*ε => F=ma.

Кинетическая энергия вращающегося твердого тела:

Ek=J*ω2/2, J - момент инерции, ω – угловая скорость тела.

5) Понятие работы и мощности. Работа переменной силы.

Работа (А) – мера измерения механической энергии бA=F*dR, dR – перемещение тела, F – сила.

Мощность (N) – скалярное произведение силы приложенной к телу на скорость тела. N=dA/dt.

Работа переменной силы –

ana13a

рассмотрим движение материальной точки вдоль оси OX под действием переменной силы f , зависящей от положения точки x на оси, т. e. силы, являющейся функцией x. Тогда работа A, необходимая для перемещения материальной точки из позиции x = a в позицию x = b вычисляется по формуле:

ana13d

Консервативные силы – работа которых не зависит от формы пути между двумя точками (при перемещении тела между ними). Все силы, не являющиеся консервативными, называются неконсервативными силами. К ним относятся, прежде всего, так называемые диссипативные силы, например силы трения, возникающие при скольжении одного тела относительно другого.

6) Основные понятия динамики вращательного движения. Момент силы и импульса.

Введем понятие абсолютно твердого тела. Будем рассматривать абсолютно твердое тело как систему жестко связанных материальных точек. При вращательном движении абсолютно твердого тела все его точки описывают окружности лежащие в плоскостях перпендикулярно оси Оz.

Момент инерции материальной точки: J=m*r2 m – масса, r – расстояние от точки до оси.

Момент силы относительно точки и неподвижной оси: Mz=F*R=Jz*ε, F – сила, R – радиус, ε – угловое ускорение.

Момент импульса относительно точки и неподвижной оси: Lz=J*ω, J – момент инерции, ω – угловая скорость.

Теорема Штейнера:

Момент инерции тела относительно произвольной оси Оz равен моменту инерции тела относительно оси Оz0 проходящей через центр масс тела параллельно оси Оz + произведение массы тела на квадрат расстояния между Оz и Оz0.

Пусть Оz0 – ось параллельная оси Оz и проходит через центр масс тела. Расстояние между осями Оz и Оz0 = d. Оси Оz и Оz0 перпендикулярны рисунку.

Jz =∑(от i = 1 до n)mi*R2i = mi*Ri*Ri. Из рисунка видно, что Ri = d + Ri0, где Ri, Ri0 – расстояния от точки mi до оси Оz, тогда: Jz =∑(от i = 1 до n)mi *( d + Ri0)2 , где =∑(от i = 1 до n)mi * Ri0 = Jz0 – момент инерции тела относительно оси Оz0 . Последнее слагаемое ∑(от i = 1 до n)mi * d* Ri0 = d*∑(от i = 1 до n)mi *Ri0 = 0 – определение центра масс Jz = M*d2 + Jz0 .

7) Потенциальная и кинетическая энергия

К механической энергии относят два вида энергии: Кинетическая и Потенциальная.

При поступательном движении кинетическая эн. Тела массой m, движущ. Тела v равна:

K=(mv2)/2.

Кинетическая энергия механической системы равна сумме кинетических энергий всех частей этой системы

Kc-мы=∑Ki=∑(mivi2)/2 ( от i=1 До n) n-число тел.

Изменение кинетической энергии системы равно работе сил, действ-х на эту систему мсо стороны др. тел или полей.

dK=∂A

Потенциальная энергия $U(\vec r)$ — скалярная физическая величина, характеризующая способность некого тела (или материальной точки) совершать работу за счет его нахождения в поле действия сил.

Энергия. Кинетическая и потенциальная энергия. Закон сохранения и изменения механической энергии.

Кинетическая энергия мех. системы - это энергия мех. движения этой системы. Работа dA силы Fна пути, который тело прошло за время возрастания скорости от 0 до V, идёт на увеличение кинетической энергии dT тела, т. е. dA = dT. Используя 2 закон Ньютона и умножая обе части равенства на перемещение dr, получим

Потенциальная энергия мех. энергия системы тел, определяемая их взаимным расположением, и характером сил взаимодействия межу ними. Работа dA выражается как скалярное произведение силы F на перемещение dr. Работа совершается за счёт уменьшения потенциальной энергии.

Полная мех. энергия системы равна сумме кинетической и потенциальной энергии. E=T+П.

Рассмотрим взаимодействие двух частиц. Пусть потенциальная энергия их взаимодействия определяется функцией U(x), где x — расстояние между частицами. Для определённости положим, что частицы отталкиваются с силой F. Под действием этой силы расстояние между частицами изменится на dx, следовательно будет совершена работа A = Fdx. При этом, поскольку частицы отодвинулись, то потенциальная энергия их взаимодействия U изменилась на величину dU (уменьшилась). Отсюда получаем

dU = F dx

или

(2)

Таким образом, в случае потенциальных сил, сила F есть производная от потенциальной энергии U по параметру x с обратным знаком.

8) Колебания. Дифференц. Ур-ия колебаний(гармонич, незатух, затух, вынужд) и их решения

Колебания-процессы, характериз-ся той или иной степенью повторяемости во времени. Они могут быть мех-ми, электромагн. И др. Колебания периодические, если они повторяются через определенные промежутки времени.

Минимальный из них это Период T. За период совершается одно полное колебание. Число полных колебаний в ед. вр. Назыв. Частотой колебаний.

f=1/T

ω=2 это круговая или циклическая частота

Период: T=

При периодический колебаниях величины x за время t выполняется след. Соотношение

X=(t)=x(t+T)

Гармоническим колебательным движением называется периодич. Движ., при котором смещение точки от положения равновесия в зависимости от времени t измен. По закону синуса

Х=Аsin(ω0t+α) (1) А-амплитуда колебания, ω0-круговая частота гарм. Колеб. (ω0t+α) - фаза колебания. Α-нач фаза в момент вр t,

Скорость v и ускорение (а) при гар. Кол. Измен-ся по закону

V==ẋ=A ω0cos (ω0t+α)

a==ẍ=-A02sin(ω0t+α)

получаем а=- ω20х

отсюда следует что при гар. Кол. Ускорение прямопропорц-но смещению точки от положения равновесия и всегда направлено противопол. Ему

Из этих уравнений получаем дифференциальное уравнение гарм. кол

ẍ+ 02=0 а уравнение (1) которое выше, является его решением

сила гар. Кол F=-m ω20x.

m ω20=k –коэффицент возвр силы. Н численно равен возвр силе, вызыв смещение х на ед.

F=-kx

Круговая частота в гар. кол : 0=

Период гар. кол: T0=2

При гар. кол полная мех. энергия складывается из кин. И пот. Энергии E = +

Затухающие колебания

Всякое колебание мат. точки, не поддерж. Извне, затухает из-за наличия сил сопротивления.

Амплитуда уменьш-ся.

Диф-ное уравнение: $\ddot{x} + { c \over m} \dot{x} + {k \over m} x = 0$

где k — коэффициент упругости в законе Гука, c — ускорение горизонтального движения грузика.

Решение его: х=А0е-βtsin(ωt+α)

Где А0е-βt-амплитуда. е - экспанента β-коэфф-т затухания α-нач фаза. ω-циклич частота затух.

Если β=0 уравнение выше переходит в уравнение незатухающих колебаний.

Β=; ω=

Период затухающих кол.:
Т=2π/ω

Логарифмический декремент затухания: ∂=ln(At/At+T)

Собственные (или свободные) — колебания при отсутствии внешних сил, когда система, после первоначального воздействия внешней силы, предоставляется самой себе (в реальных условиях свободные колебания всегда затухающие)

Если ω меньше или равна 0 то колебаний нет. система совершает апериодические колебания. Приближ к равновесию.

Вынужденные кол. — колебания, происходящие под воздействием внешних сил, меняющихся во времени.

Сила в этом случае

F=-kx-rẋ+F0sinΏt

По 2-му зак Ньютона

ẍ+0sinΏt/m это дифференциальное уравнение вынужденных коллебаний

Решение его: х=А0е-βtsin(ωt+α)+Asin(

Вынужденные складываются из затух и незатух. Происходящих с частотой Ώ.

Установившиеся вынужд кол. Х= Аsin(Ώt+Ѱ)

Амплитуда вынуж. Кол. А=F0/m*(sqrt[(ω02-Ώ2)2+4β2Ώ2])

Где ω0=sqrt(k/m) частота собст колеб, β=r/2m-коэфф. Затух

9) Термодинамические и статистические методы исследование термодинамич.

Систем. Давление и темпер. Идеал. газа. Понятие о равновеном процессе. Уравнение состояния идеального газа. Изопроцессы.

Термодинамич. Системы состоят из большого числа частиц.

Термодинамич. Метод исследов. Основан на описании состояния системы с помощью некоторых макроскопических параметровЮ, характер-х состояние системы в целом к ним относят оббьем, давление, температуру.

Термодинамика изучает равновесные состояние вещества, при которых термодин. Параметры вещ-ва остаются пост. И равными своим средним значениям по всему обьему..

Число частиц: N=vNA где NA-число авагадро(6.02*1023) v-кол-во вещества.

v=m/μ где μ-молярная масса в-ва.

Идеальный газ – это газ молекулы которого можно рассматривать как материальные точки, взаимодействие которых между собой происходит только в момент соударения.

Уравнение состояния(Клапейрона-Мендлеева)- PV=RT, gde m-масса газа, R – универс. газ. пост.(8.31 дж/к*моль)

Для 1 моля уравнение такое : PV=RT

Переход термодин. системы из одного состояния в другое называется термодин. процессом.

Изохорический процесс(V-const) закон Шарля.

P/T=const.

Изобарический проц. P-const закон Гей-люссака V/T=const

Изотермический проц.(T=const) закон Бойля-Мариотта PV=const

Равнове́сный тепловой процесс — тепловой процесс, в котором система проходит непрерывный ряд бесконечно близких равновесных термодинамических состояний.

Равновесный тепловой процесс называется обратимым, если его можно провести обратно и в телах, окружающих систему, не останется никаких изменений.

Реальные процессы изменения состояния системы всегда происходят с конечной скоростью, поэтому не могут быть равновесными. Реальный процесс изменения состояния системы будет тем ближе к равновесному, чем медленнее он совершается, поэтому равновесные процессы называют квазистатическими.

10) первое начало термодинамики, внутренняя энергия ид. Газа. Теплота. работа.

∂Q=dU+∂A это 1-е начало термод. Означает что количество теплоты подеденное к системе расходуется на изменение энергии и совершение работы.

Количество теплоты положительное если оно подводится к системе и отрицательно если отводится.

Внутрення энергия системы является функцией состяния и не зависит от вида процесса. Бесконечно малое изменение внутр. эн. dU является полным дифференциалом т. е.

∆U1-2==U2-U1

Количество теплоты и работа не являются функциями состояния и зависят от способа перехода системы. Поэтому ∂Q и ∂A не явл. Полными диффер-ми.

Элем-ая работа газа при малом изменении его обьема записано так: ∂A=PdV

Из состояния 1 в 2 выглядит так: A1-2=

Работа газа положительна, если в процессе происходит расширение газа(обьем увелич) и отрицательна при уменьшении обьема газа.

11) Адиабатический процесс. Уравнение Пуассона. 1-е начала термодинамики для Адиабат. процесса

Адиабатический процесс – это процесс расширения газа, при котором выполняется 2 условия: а) внешнее давление постоянно и равно давлению самого газа, б) газ остаётся теплоизолированным.

При адиабатическом процессе бQ = 0, U <> const, бА = - dU

Адиабатический процесс описывается уравнением Пуассона: P*Vγ = const.

Адиабатическое расширение сопровождается охлаждением, а сжатие нагреванием.

Первое начало термодинамики для адиабатического процесса: бQ = 0, А = -ΔU. Первое начало термодинамики говорит о возможности создания вечного двигателя первого рода.

12) Вероятностное описание случайных событий. Функция распределения Максвела по модулю скорости

Рассмотрим систему из N молекул заполняющую некоторый объем V. Разобъем пространство на бесконечно – малые объемы dV, тогда число dN молекул в нем определяется следующим соотношением dW=dN/N есть вероятность, что первая произвольная выбранная молекула газа в момент времени t окажется в объеме dV.

W(t, r) = dW/dV – плотность вероятности или функция распределения молекул в пространстве. Для описания микроскопического состояния газа используют функции f = f(t, r,v). Функция распределения Максвелла дает распределение по скорости молекул в газе. F(v) = 4π(α/π)3/2 *v2 * exp(-α* v2).

Физический смысл функции Максвела заключается в следующем: в соответствии с определением вероятности выражения f(v)dv, модуль скоростей которые лежат в интервале(v, v+dv) при этом относительное кол-во молекул скорости которые лежат в интервале от V1 до V2 будет выражено: N{V=[V1,V2]}/N=

13. Распределение Больцмана. Барометрическая формула.

Постоянная Больцмана (k или kb) — физическая постоянная, определяющая связь между температурой и энергией. Названа в честь австрийского физика Людвига Больцмана, сделавшего большой вклад в статистическую физику, в которой эта постоянная играет ключевую роль. Её экспериментальное значение в системе СИ равно

k=1,380,650,4(24)* 10^{-23} Дж/К.

Числа в круглых скобках указывают стандартную погрешность в последних цифрах значения величины. Постоянная Больцмана может быть получена из определения абсолютной температуры и других физических постоянных. Однако, вычисление постоянной Больцмана с помощью основных принципов слишком сложно и невыполнимо при современном уровне знаний. В естественной системе единиц Планка естественная единица температуры задаётся так, что постоянная Больцмана равна единице.

Универсальная газовая постоянная определяется как произведение постоянной Больцмана на число Авогадро, R = kNA. Газовая постоянная более удобна, когда число частиц задано в молях.

Барометрическая формула — зависимость давления или плотности газа от высоты в поле тяжести. Для идеального газа, имеющего постоянную температуру T и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного падения g одинаково), барометрическая формула имеет следующий вид:

$p=p_0\exp\left[-Mg\frac{h-h_0}{RT}\right],$

где p — давление газа в слое, расположенном на высоте h, p0 — давление на нулевом уровне (h = h0), M — молярная масса газа, R — газовая постоянная, T — абсолютная температура. Из барометрической формулы следует, что концентрация молекул n (или плотность газа) убывает с высотой по тому же закону:

$n=n_0\exp\left[-mg\frac{h-h_0}{kT}\right],$

где m — масса молекулы газа, k — постоянная Больцмана.

Барометрическая формула может быть получена из закона распределения молекул идеального газа по скоростям и координатам в потенциальном силовом поле (см. Статистика Максвелла — Больцмана). При этом должны выполняться два условия: постоянство температуры газа и однородность силового поля.

15. Второе начало термодинамики (его формулировки). Принцип работы тепловой машины. Цикл Карно.

Второе начало термодинамики: в процессах, происходящих в замкнутой системе, энтропия не убывает.

По Кельвину: невозможен круговой процесс единственным результатом которого является превращение теплоты полученной от нагревателя, в эквивалентную ей работу.

По Клаузиусу: невозможен круговой процесс единственным результатом которого является передача теплоты от менее нагретого тела к более нагретому.

Принцип действия тепловой машины: от термостата с более высокой температурой Т1 наз. нагревателем за цикл отнимается кол-во теплоты Q1, а термостату с более низкой температурой Т2 наз. холодильником, за цикл передается кол-во теплоты Q2, при этом совершается работа A=Q1-Q2 .

Принцип действия холодильной машины: за цикл от термостата с более низкой температурой Т2 отнимается кол-во теплоты Q2 и отдаётся термостату с более высокой температурой Т1 кол-во теплоты Q1 .

Без совершения работы нельзя отбирать теплоту от менее нагретого тела и отдавать её более нагретому.

Цикл Карно.

1-2 и 3-4 - изотермическое расширение и сжатие, 2-3 и 4-1 - адиабатическое расширение и сжатие.

Термический КПД цикла Карно

Записав для адиабат

16. Применение 1-ого начала термодинамики к изопроцессам. Работа расширения газа в изопроцессах.

В изотермическом процессе температура постоянная, следовательно, внутренняя энергия не меняется. Тогда уравнение первого закона термодинамики примет вид: Q=A’, т. е. количество теплоты, переданное системе, идет на совершение работы при изотермическом расширении, именно поэтому температура не изменяется.

В изобарном процессе газ расширяется и количество теплоты, переданное газу, идет на увеличение его внутренней энергии и на совершение им работы:Q=ΔU+A’.

При изохорном процессе газ не меняет своего объема, следовательно, работа им не совершается, т. е. А = 0, и уравнение первого закона имеет вид Q= ΔU, т. е. переданное количество теплоты идет на увеличение внутренней энергии газа.

Адиабатным называют процесс, протекающий без теплообмена с окружающей средой. Q = 0, следовательно, газ при расширении совершает работу за счет уменьшения его внутренней энергии, следовательно, газ охлаждается, A’= ΔU Кривая, изображающая адиабатный процесс, называется адиабатой.

1) Изотермическое сжатие

Для вывода 1 закона термодинамики воспользуемся интерактивной моделью изотермического сжатия ( рис.2) и графическим истолкованием работы для процесса ( рис.3)

рис. 2 рис.3 рис.4

Для изотермического процесса T - const, T=0, а значит U= 3/2 v RT=0 ( внутренняя энергия не изменяется). Над газом совершается работа А>0, а тепло выделяется Q<0.

Первый закон термодинамики U=A+Q выглядит так:

0 = - Q + A

Над газом совершается работа, при этом газ выделяет тепло во внешнюю среду ( внутренняя энергия не изменяется)

А блок –схема 1 закона для изотермического сжатия приведена на рис. 4

2) Изотермическое расширение

Для вывода 1 закона термодинамики воспользуемся интерактивной моделью изотермического расширения ( рис.5) и графическим истолкованием работы для процесса( рис.6)

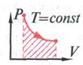
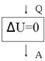
рис.5 рис.6 рис.7

Для изотермического процесса T - const, T=0, а значит U=0 ( внутренняя энергия не изменяется). Газ совершает работу А<0, а тепло поглощается (Q>0).

Первый закон термодинамики выглядит так:

Q = A

Газ совершает работу за счет поглощения тепла из внешней среды ( внутренняя энергия не изменяется)

Блок - схема первый закона термодинамики для изотермического сжатия представлена на рис. 7

3) Изобарное нагревание.

Воспользуемся интерактивной моделью и (пронаблюдаем изобарное нагревание) ( рис. 8) и графическим представлением работы ( рис. 9)

рис.8 рис.9 рис.10

При изобарном нагревании температура увеличивается ( T>0 ), внутренняя энергия увеличивается (U>0), газ совершает работу, тепло поглощается.

Первый закон термодинамики выглядит так:

Q = U – A

Газ получает тепло из внешней среды. Полученная таким образом энергия тратится на увеличение внешней энергии и на совершение работы.

В итоге блок - схема первого закон термодинамики выглядит как на рис.10

4) Изобарное охлаждение

Пронаблюдав процесс изобарного охлаждения на интерактивной модели ( рис.11) и воспользовавшись рис.12 можем сделать вывод:

рис.11 рис.12 рис.13

при изобарном охлаждении температура уменьшается ( T<0 ), внутренняя энергия уменьшается ( U<0), над газом совершается работа, тепло выделяется.

Первый закон термодинамики выглядит так:

U = - Q + A

Над газом совершается работа, при этом газ выделяет тепло во внешнюю среду, а его внутренняя уменьшается.

Блок – схема для 1 закона термодинамики для этого случая представлен на рис. 13

5) Изохорное нагревание

Изохорное нагревание пронаблюдаем на интерактивной модели ( рис14) и воспользуемся графиком на рис 15. Вывод:

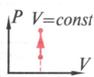
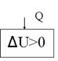
рис. 14 рис. 15 рис. 16

При изохорном нагревании ( T>0 ), внутренняя энергия увеличивается (U>0) , работа A=pV равна нулю, т. к. V=0, а тепло поглощается (Q>0).

Первый закон термодинамики выглядит так:

U=Q

Газ увеличивает свою внутреннюю энергию за счет теплоты, полученной из внешней среды.

Интерпретация 1 закона термодинамики для изохорного нагревания представлена на рис. 16

6) Изохорное охлаждение

Изохорное охлаждение пронаблюдаем на интерактивной модели ( рис17) и графиком на рис 18. Вывод:

рис. 17 рис. 18 рис. 19

При изохорном охлаждении ( T<0 ), внутренняя энергия уменьшается(U<0 , работа A=pV равна нулю, т. к. V=0, а тепло выделяется (Q<0).

Первый закон термодинамики выглядит так:

- U=-Q

Газ выделяет тепло во внешнюю среду; при этом его внутренняя энергия уменьшается.

17. Теплоёмкость.

Теплоемкостью какого-либо тела наз. величина, равная кол-ву тепла, которое нужно сообщить телу, чтобы повысить его тем-ру на 1 кельвин. (дж/К)

Теплоемкость моля вещества наз. молярной теплоемкостью, обозначают (С=Дж/моль*К)

Теплоемкость единицы массы вещества наз. удельной теплоемкостью, обозначают (с=С/М где

М - молярная масса). Величина теплоемкости зависит от условий, при которых происходит нагревание тела. Различают теплоемкость при постоянном объёме Сv, и при постоянном давлении Ср. Между удельной и молярной теплоёмкостью имеется соотношение с=С/М.

18. Характерные скорости движения молекул газа. Вычисление средних скоростей в статической физики.

По определению среднее значение какой-то величины, которая случайным образом в N независимых испытаниях принимает N значений ai, равно

Ввиду полной хаотичности движения молекул проекции скорости молекул на ось x с равной вероятностью могут принимать как положительные, так и отрицательные значения. Поэтому среднее значение проекции скорости i-ой молекулы на ось x равно нулю: <vix>=0. Аналогично <viy>=<viz>=0. Однако средние значения квадратов проекций скорости не равны нулю! Определим для i-ой молекулы

vi2 = vix2 + viy2 + viz2.

Тогда

формула2

Поскольку все направления эквивалентны, то

<vx2> = <vy2> = <vz2>,

поэтому

< vx2> = < v2>/3.

Уравнение среднеквадратичной скорости молекулы легко выводится из основного уравнения МКТ для одного моля газа.

$E_k = \frac{1}{2}Nm\bar{v^2} = \frac{3}{2}RT$ , для 1 моля N = Na, где Na — постоянная Авогадро

Nam = Mr, где Mr — молярная масса газа

Отсюда окончательно

$\bar{v} = \sqrt{\frac{3RT}{M_r}}$

19. Принцип относительности в классической и релятивистской механике. Постулаты Эйнштейна. Преобразования Лоренца.

Механический принцип относительности Галилея.

При описании физических явлений мы всегда пользуется какой-либо системой отсчета. Например, движение тел мы чаще всего рассматриваем относительно земли, т. е. условно принимаем земной шар за неподвижное тело.

Галилей показал, что в условиях земли практически справедлив закон инерции. Такую систему отсчета, в которой выполняется закон инерции стали называть инерциальной. Теперь рассмотрим две системы отсчета, движущиеся друг относительно друга с постоянной скоростью V0 . Одну из этих систем, обозначенную на рисунке буквой К будем условна считать неподвижной. Тогда вторая система К' будет двигаться прямолинейно и равномерно.

Найдем связь между координатами x, y,z некоторой точки Р в системе К и координатами x',y',z' так же точки в системе К'. Если начать отсчет времени с того момента, когда начала координат обеих систем совпадали, то x=x'+v0t (1). Кроме того, что y=y' и z=z' (2).

Добавив и этим соотношениям принятое в классической механике предположение, что время в обоих системах течет одинаковым образом, т. е. что t=t', и получим совокупность четырех уравнений: x=x'+v0 t ; y=y'; z=z' ; t=t' (3); называемых преобразованием Галилея.

Продифференцировав эти отношения, найдем связь между скоростями точки Р по отношению и системам отсчета К и К': (4); (5); (6) или (7), ; (8). Эти соотношение дают правило сложения скоростей в классической механике. С одним словом Г. Галилей ввел в классическую механику принцип относительности, смысл которого следующий: никакими механическими опытами нельзя установить, покоится инерциальная система отсчета или движется равномерно и прямолинейно.

Все выше сказанное справедливo лишь при значениях , малых сравнению со скоростью света в вакууме, которую мы будем обозначать буквой С . При больших скоростях , сравнимых с С, для изучения движения тел, создали новая механика, которая включить себя классическую механику Ньютона как частный, предельный случай и называли релятивистической механикой.

Постулаты специальной теории относительности.

Для описания движений, совершающихся со скоростями, с равными с. С, Эйнштейн создал релятивистическую механику, т. е. механику, учитывающую требование специальной теории относительности.

Основу этой теории образуют два постулата, которые носят названия принципа относительности Эйнштейна и принципа постоянства скорости света. Согласно принципа относительности Эйнштейна все законы природы одинаковы во всех инерциальных системах отсчета.

Принцип постоянства скорости света утверждает, что скорость света в вакууме одинакова во всех инерциальных системах отсчета и не зависит от движения источников и приёмников света.

Преобразование Лоренца.

Рассмотрим две инерциальные системы отсчета, которые мы обозначим К и К'. рис. Предположим, система координат К' движется относительно системы К с постоянной скоростью v. Распространение светового сигнала в положительном направлении оси х описывается уравнением: (9). Для системы координат К' аналогичное уравнение имеет вид: (10).

Движению, происходящему в обеих системах координат, должны удовлетворять как уравнение (9), так и уравнение (10), что выполняется, если имеет место соотношение: (11), где l-постоянная величина. Для лучей, распространяющихся в отрицательном направлении оси Х, уравнение (11) имеет вид: (12), где m-постоянная величина. Введем новые постоянные: (13), (14). Тогда, (15), (16). Определим постоянные а и в.

Для начала координат системы К' имеем x'=0, тогда (16) или (17).
Если в уравнение (15) положить t=0, t0 x'=ax (18) . Из этого следует, что если некоторый отрезок в системе К' равен единице то, наблюдая его из системы К, мы обнаружим, что (19). Если в системе К', t'=0, то и (20). Так как оба наблюдения должны быть идентичными, то , или (21). Это равенства определяют постоянные а и в. Подставляя их значения в уравнения (15) и (16), получаем: (22) и времени: (23).К этим соотношениям можно добавить уравнения y'=y, z'=z (24).< br>

Рассмотрим некоторые выводы из теории относительности, вытекающие из преобразования Лоренца.

1. Из преобразований Лоренца для координат х и x' и времени t и t' следует, что . В противном случае эти координаты и времена окажутся мнимыми. Скорость v относительного движения двух инерциальных систем отсчета не может превосходить скорости света в вакууме.

2. Пусть стержень MN движется вместе с системой отсчета K' относительно системы К. рис. Длина стержня в системе К' равна: (25). Длина тела в системе отсчета, где оно покоится , называется собственной длиной. Для определения длины движущегося стержня в системе К необходимо найти координаты х2 и х1 точек N и M конца и начала стержня в один и тот же момент времени по часам в системе К': (26). Из преобразований Лоренца следует, что (27), или (28). Длина тела зависит от скорости его движения. Собственная длина тела является его наибольшей длиной. Линейный размер тела, движущегося относительно инерциальной системы отсчета уменьшается в раз. Из преобразований Лоренца следует, что и (29), т. е. поперечные размеры тела не зависит от скорости его движения и одинаковы во всех инерциальных системах отсчета.

3. Время измеряемое в системе отсчета, где точка неподвижна, назы-вается собственным временем. В системе К, относительно которой система К' движется промежуток времени t между событиями будет: t=t2 - t1 (30), где время отсчитано по часам в системе К. Из преобразований Лоренца для времени: (31) и (32). Следует, что (33). Но смещение точки вдоль оси ОХ системы К за время t: и (34), т. е. или (35). Длительность явления, происходящего в некоторой точке пространства, будет наименьшей в той инерциальной системе отсчета, относительно которой эта точка неподвижна эта означает, что часы движущиеся относительно инерциальной системы отсчета, идут медленнее неподвижных часов и показывает меньший промежуток времени между событиями.

4. Релятивистский закон сложения скоростей. Если материальная точка движется вдоль осей ОХ и О'X' в инерциальных системах К и К' и имеет в этих системах скорости, равные соответственно v и v' , то (36), где V - скорость движения системы К'относительно системы К.

Релятивистская динамика.

Одним из основных законов классической механики является закон сохранения количества движения: . В релятивистская динамики масса тела определяется по формуле: (37), где - . Выражение импульса в соответствии с (37) имеет более сложный вид: (38). Тогда уравнение релятивистской динамики будет иметь вид: (39).
Энергии движущегося тела в релятивистской динамике растет его со скоростью быстрее, чем в классической механике. Однако возрастание энергии, так же как и в классической механике, вызывается работой силы F: (40).Отсюда (41). Подставляя (37) в (41) получим: (42), откуда после интегрирования получим: (43).
Если приравнять постоянную интегрирования нулю, то получим энергию, эквивалентную массе покоя, т. е. (44). Полная энергия движущегося тела равна: (45). Эта уравнение выражает закон взаимосвязи массы и энергии: полная энергия системы равна произведению ее полной релятивистской массы на квадрат скорости света в вакууме.