СОДЕРЖАНИЕ
Введение
1 Кинематический анализ рычажного механизма
1.1 Кинематическая схема машинного агрегата
1.2 Кинематическая схема исполнительного механизма
1.3 Структурный анализ строгального станка
1.4 План положений
1.5 План скоростей
1.6 План ускорений
1.7 Построение диаграммы перемещений
1.8 Построение диаграммы скоростей
1.9 Построение диаграммы ускорений
ВВЕДЕНИЕ
В строгальных станках движение подачи имеет заготовка или резец. Станки этой группы служат для обработки разнообразных линейчатых поверхностей, описанных прямой, перемещающейся по направляющей линии, в соответствии с рисунком 1. Относительное перемещение заготовки и инструмента по направляющей – линии обеспечивается движением подачи, а по образующей — движением резания. Движение резания поперечно – и продольно – строгальных станков – всегда горизонтальное.
Поперечно – строгальные станки применяют в единичном и серийном производстве для обработки небольших по размерам заготовок. Продольно – строгальные станки позволяют обрабатывать станины станков корпусные детали и т. п.
Рисунок 1 – Виды работ, выполняемых на строгальных станках
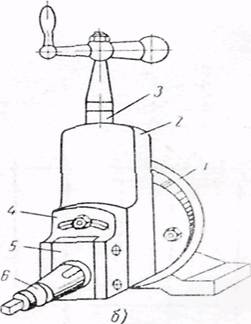
На рисунке 2 а) показан общий вид поперечно – строгального станка. В верхних направляющих станины 1 смонтирован ползун 2, совершающий с помощью кулисного механизма возвратно – поступательное перемещение (главное движение). На левом конце ползуна укреплен суппорт 3. Он состоит из поворотного диска 1 показанных на рисунке 2 б) и салазок 2, получающих периодически вертикальную подачу от ходового винта 3. На салазках смонтирована резцовая каретка 4 с откидной планкой 5 и резцедержателем 6.
|
|
На вертикальных направляющих станины (слева) находится поперечина 4 в соответствии с рисунком 2 а), по которой в горизонтальной плоскости перемещается стол 5 (движение подачи). На верхнюю плоскость стола устанавливают заготовки или тиски и закрепляют их с помощью болтов, устанавливаемых в Т – образные пазы стола.
Рисунок 2 - Поперечно–строгальный станок
Плоскости обрабатывают следующим образом. Стол 5 с поперечиной устанавливают на определенной высоте в зависимости от вертикального размера заготовки. Для большей жесткости стол дополнительно закрепляют в стойке 6. Процесс строгания, происходит при движении ползуна влево. По окончании рабочего хода ползун возвращается направо, совершая ускоренный холостой ход, в конце которого механизм 7 осуществляет периодическую подачу стола вдоль направляющих поперечин. При отрезных операциях или при обработке вертикальных плоскостей периодическую подачу совершает суппорт 3.
В двухстоечном продольно – строгальном станке в соответствии с рисунком 3, стол 3 с помощью реечной передачи перемещается по призматическим направляющим 1 станины 2. На рабочей плоскости стола устанавливают и закрепляют заготовки. По обе стороны станины расположены боковые стойки 4 и 5, скрепленные для жесткости поперечной балкой 6. В вертикальных направляющих стоек смонтирована траверса 7, несущая два резцовых суппорта 8 с резцедержателями. С правой стороны станка размещены агрегаты привода. В зависимости от вертикальных размеров заготовок траверсу устанавливают на определенной высоте и зажимают. При строгании стол совершает возвратно – поступательное движение. В конце рабочего хода осуществляется периодическая подача верхних суппортов 8 в горизонтальном, а боковых суппортов 9 — в вертикальном направлении. В связи с этим резцы, установленные в резцедержателях суппортов 8, обрабатывают горизонтальные плоскости или линейчатые поверхности, а в суппортах 9 — боковые.
Рисунок 3 - Продольно – строгальный станок
1 КИНЕМАТИЧЕСКИЙ АНАЛИЗ РЫЧАЖНОГО МЕХАНИЗМА
1.1 Кинематическая схема машинного агрегата
Рисунок 4 - Кинематическая схема машинного агрегата
1.2 Кинематическая схема исполнительного механизма
1 – станина, 2 – кривошип AB, 3 - ползун В, 4 – коромысло СD, 5 – коромысло DE, 6 – ползун E.
Рисунок 5 - Кинематическая схема исполнительного механизма
1.3 Структурный анализ строгального станка
Под структурным анализом механизма понимают определение количества звеньев и кинематических пар, определение степени подвижности механизма, а также установление класса и порядка механизма.
Структурный анализ преследует цели:
1.Выявление условий, при выполнении которых рассматриваемая кинематическая цепь преобразуется в механизм с определённым движением вне звеньев.
2.Результат структурного анализа даёт возможность путём определения класса и порядка рассматриваемого механизма подобрать общие для этого класса и порядка методы исследования групп механизмов.
3.Выявление избыточных связей в механизме.
Структурный анализ выполняется по правильно составленной структурной схеме механизма. Структурная схема должна отображать принцип действия механизма и основные особенности работы. Наиболее удачным методом нахождения структурной схемы механизма является метод присоединения структурных групп Ассура к ведущему звену или основному механизму. Группа Ассура - это кинематическая цепь, состоящая из n-числа звеньев, соединённых между собой кинематическими парами пятого класса таким образом, что степень подвижности этой цепи равна нулю.
1 – стойка, 2 – кривошип, 3 – шатун, 4 – кулиса, 5 – камень кулисы
Рисунок 6 – Рычажный механизм строгального станка
Проводим структурный анализ и устанавливаем класс механизма. Число звеньев k=6, число подвижных звеньев n=5, число кинематических пар V класса p5=7, степень подвижности механизма /3, с 52./:
W=3n – 2p5 =1 (1)
Значение W=1 означает, что на механизм будет приводиться в движение одним двигателем.
Таблица 1 - Структурный анализ механизма
Механизм образован так: к ведущему звену АВ и стойке 1 присоединена группа Ассура второго класса второго вида, состоящая из звеньев 2 и 3, а к этой группе и стойке присоединена группа второго класса второго вида, состоящая из звеньев 4 и 5, следовательно, данный механизм следует отнести ко второму классу.
1.4 План положений
Для построения плана положений вычислим масштабный коэффициент – это отношение действительной величины к длине отрезка на чертеже. Масштабный коэффициент плана положений обозначается:
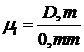(2)
При исследовании кинематики рычажных механизмов масштабный коэффициент удобно выбирать через длину кривошипа, учитывая ограничения:
1. 
должен быть выбран таким образом, чтобы планы положений механизма занимали бы на чертеже площадь не более одной четверти листа формата А1;
2. Выбранное значение должно соответствовать стандартному значению масштаба.
В нашем случае для построения плана положений рычажного механизма пресса выбираем масштабный коэффициент, соответствующий:
µl=LAB/AB=0,12/60=0,002 м/мм, (3)
где 
- действительная величина кривошипа;
AВ - величина звена на чертеже
Таким образом, длины звеньев на чертеже получим делением на масштабный коэффициент:
LCD=0,18 м;
CD=0,18/0,002=90 мм
Аналогично для остальных звеньев механизма:
LDE= 0,5 м,
DE=0,5/0,002=250 мм;
L1=0,03 м,
L’1=0,03/0,002=15 мм.
В большинстве современных производственных машин технологический процесс осуществляется периодически и характеризуется определенными циклами (цикл – совокупность явлений, проходящих полный круг своего развития). Механизмы машины совершают движение либо в течении всего времени цикла технологического процесса, либо в некоторой его части. Рычажные механизмы в своем большинстве являются механизмами циклического действия. Интервал цикла, на котором происходит выполнение технологической операции, называют фазой рабочего цикла. Интервал цикла, на котором звенья механизма перемещаются без выполнения полезной работы, называют фазой холостого хода. В период рабочего хода выходное звено воздействует на обрабатываемый материал или среду. В течение холостого хода выходное звено возвращается в исходное положение для повторения нового рабочего хода.
Деление полного цикла работы механизма на рабочий и холостой ход обуславливает появление двух крайних положений выходного звена. Удобнее начинать построение планов положений механизма с крайних положений.
За нулевое положение принимаем одно из двух крайних положений таким образом, чтобы шестое звено двигалось в направлении стрелки рабочего хода. Определяем угол рабочего хода: в данном случае он равен углу холостого хода и составляет 180º. Радиусом, равным AB, проводим окружность и делим её на 12 равных частей и получаем точку B. Проводим окружность радиусом равным CD из точки C. Проводим лучи из точки C через точки B до пересечения с окружностью радиусом CD. Теперь из точек D делаем засечки радиусом DE по прямой движения ползуна E по оси x-x.
1.5 План скоростей
Рассмотрим построение планов скоростей на примере седьмого положения. Строить будем в масштабе кривошипа /3, с 55./.
Начинаем построение с группы, состоящей из звеньев 2 и 3, так как она непосредственно присоединена к ведущему звену и стойке. Запишем векторное уравнение для нахождения скорости точки В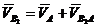2 :
, (2)
где 
- скорость точки А, равная нулю;
- скорость точки В2 относительно точки А, направленная перпендикулярно АВ в соответствии с направлением угловой скорости ω2, по модулю равная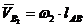 
.
Так как кривошип 1 и камень кулисы 2 связаны между собой вращательной кинематической парой, то не допускается линейных относительных перемещений, и значит линейные скорости звеньев, соединенных в этой точке, равны между собой, то есть 
.
Далее запишем векторные уравнения для нахождения скорости точки В4, принадлежащей кулисе 3:
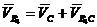, (3)
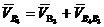, (4)
где 
- скорость точки С, равная нулю;
- скорость точки В4 во вращении звена 3 относительно точки С, по
модулю равная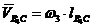 
и направленная перпендикулярно ВС
(пока нам не известная);
- скорость точки В4 относительно точки В2(В3), направленная
параллельно линии ВС.
Строим решение векторного уравнения (3) и (4). От полюса р плана откладываем отрезок (pb), изображающий скорость . Длину этого отрезка принимаем равной (pb)=(2*АВ)=120 мм, то есть строим план увеличенным в два раза. Через точку b2(b3) проводим направление скорости - линию, параллельную СВ4. Переходим к построению решения уравнения (6). Надо отложить вектор скорости точки С, но так как его модуль равен нулю, то конец его помещаем в полюс плана р и из очки р проводим направление скорости - линию, перпендикулярную СВ. Пересечение ее с раннее проведенной линией, параллельной СВ, дает конец вектора скорости 
- точку b4. Точку d – конец вектора скорости точки D – находим по правилу подобия из соотношения:
, (5)
откуда
(6)
Переходим к построению плана скоростей группы 4, 5. Также учтем, что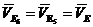 
. Этот план строим по уравнениям:
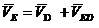(7)
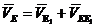, (8)
где 
- скорость точки Е;
- скорость точки D (ее вектор отложен на плане скоростей в виде
отрезка (pd));
- скорость точки Е во вращении звена 4 относительно точки D, по
модулю равная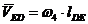 
и направленная перпендикулярно
линии DE (пока нам не известна);
- скорость точки звена 1, модуль ее равен нулю, так как звено 1
неподвижно;
- скорость точки Е относительно точки Е1, направленная параллельно
линии х – х.
Построение сводится к проведению через точку d (согласно уравнению (7)) линии, перпендикулярной DE, то есть направлению скорости 
и проведению через точку р (согласно уравнению (8)) линии, параллельной х-х. Точка е пересечения этих линий есть конец вектора скорости точки Е. Помещаем в полюс точки а, с, е1 и на этом заканчиваем построение плана скоростей механизма. Аналогичные построения проводим для оставшихся одиннадцати положений. Пример построения плана скоростей изображен на рисунке 7.
Рисунок 7 – Пример построения плана скоростей
Далее рассчитаем угловую скорость кривошипа 1:
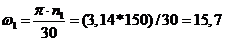с-1, (10)
где ω1 – угловая скорость кривошипа AB.
Теперь найдём масштабный коэффициент, необходимый для построения планов скоростей:
мм/(м/с) (11)
Нахождение истинного значения скорости точки Е:
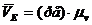м/с (12)
1.6 План ускорений
Планы ускорений строят по составленным векторным уравнениям, точно в такой же последовательности с использованием тех же самых приёмов, как и при построении планов скоростей.
Начинаем построение с группы, состоящей из звеньев 2 и 3, так как она непосредственно присоединена к ведущему звену и стойке. Запишем векторное уравнение для нахождения скорости точки В2:
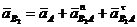, (13)
где 
;
, так как движение входного звена принимаем равномерным;
- нормальное ускорение точки В2, по модулю равное 
и
направленное параллельно АВ от точки В2 к точке А.
Также заметим, что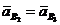 
по указанной выше причине.
Переходим к построению плана ускорений группы 3 и 4. Построение ведем по следующим векторным уравнениям:
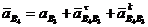(14)
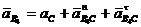, (15)
где 
- ускорение точки В4, которая принадлежит звену 4;
- относительное ускорение точки В4 относительно точки В3,
направленное параллельно линии СВ;
- ускорение Кориолиса в движении точки В4 относительно звена 3,
по модулю равное
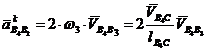(16)
и имеющее направление вектора относительной скорости 
, повернутого на 90º в направлении угловой скорости ω3 переносного движения (движения звена 3);
- ускорение точки С, равное нулю;
- нормальное ускорение точки В4 во вращении звена 4 относительно
точки С, по модулю равное
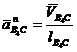(17)
и направленное параллельно линии СВ4 от точки В4 к точке С;
- касательное ускорение точки В4 в том же движении звена 4, по
модулю равное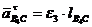 
(нам пока не известно) и направленное
перпендикулярно СВ4.
Строим решение векторного уравнения (14). Задаемся отрезком (πр)=(2*АВ)=120 мм, который изображает в плане ускорение 
. Выбранный отрезок (πр) откладываем от полюса (π), далее к нему прибавляем отрезок (bk) – вектор кориолисова ускорения – его длину находим по формуле
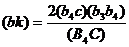мм , (18)
где отрезки (b4c) и (b3b4) взяты из плана скоростей, а отрезок (B4C) из плана положений. Через точку k проводим направление ускорения 
- линию, параллельную СВ4.
Переходим к построению векторного уравнения (15). Точку с совмещаем с точкой π, так как 
, от точки π откладываем отрезок (πnB4C), изображающий нормальное ускорение , его длина равна
мм (19)
Далее через точку nB4C проводим направление ускорения - линию, перпендикулярную СВ, до пересечения с ранее проведенной через точку k линией, параллельной СВ. Точка пересечения b4 представляет собой конец вектора ускорения . Конец вектора ускорения центра шарнира D (точку d) найдем по правилу подобия из соотношения
мм (20)
Переходим к построению ускорений группы 4 и 5 по уравнениям:
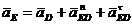(21)
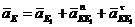, (22)
где 
- ускорение точки Е; 
- ускорение точки D;
- нормальное ускорение точки Е во вращении звена 5
относительно точки D и направленное параллельно линии
ED от точки Е к точке D; 
- касательное
ускорение той же точки в том же движении звена 5,
направленное перпендикулярно линии ED;
- ускорение точки Е1, которая принадлежит звену 1, равное нулю;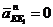 
, так как 
;
- относительное ускорение точки Е относительно стойки,
направленное параллельно линии х-х.
В соответствии с векторным уравнением (21) от точки d откладываем отрезок (dnED), изображающий нормальное ускорение 
. Его длина равна
мм (23)
Далее через точку nED проводим направление ускорения 
- линию, перпендикулярную ED) и переходим к построениям по векторному уравнению (22). В точку π помещаем точку е1, так как 
. Из точки π проводим направление ускорения (линию, параллельную х-х) до пересечения с линией, раннее проведенной из точки nED . Точка пересечения e является концом вектора ускорения точки Е, то есть ускорения . Располагаем в полюсе точку а и на этом заканчиваем построение плана ускорения механизма. Аналогичные построения проводим для оставшихся одиннадцати положений. Пример построения плана ускорений изображен на рисунке 8.
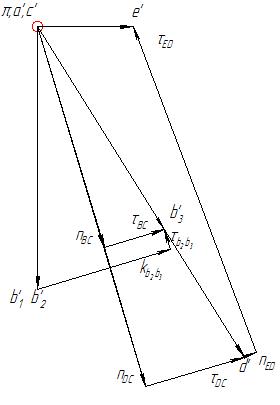
Рисунок 8 – Пример построения плана ускорений
Теперь найдём масштабный коэффициент, необходимый для построения планов ускорений:
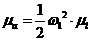(24)
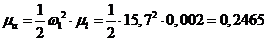мм/(м/с2)
Нахождение истинного значения ускорения точки Е:
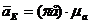м/с2 (25)
Истинные значения ускорений точки Е для оставшихся положений:
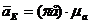м/с2 (26)
1.7 Построение диаграммы перемещения
Данный метод основан на применении графического дифференцирования функций положения S(φ), где φ – угол поворота кривошипа.
ms=0,004 м/мм
Диаграмма перемещений выходного звена строится следующим образом: по оси абсцисс откладываем обобщенную координату, то есть угол перемещения входного звена, таким образом, через 300 получаем 12 точек. По оси ординат откладываем перемещение выходного звена в масштабе кривошипа в зависимости от угла поворота входного звена. При угле 
= 0 перемещение точки Е равно нулю, при угле =300 точка Е перемещается на некоторое расстояние, которое мы прибавляем к предыдущему значению перемещения точки Е и откладываем полученное значение при соответствующем значении угла f. Значение перемещения точки Е при других углах определяется аналогичным образом. Диаграмма перемещений показана на рисунке 9.
Рисунок 9 – Диаграмма перемещений
1.8 Построение диаграммы скоростей
Диаграмма перемещений, построенная ранее служит основной для построения диаграммы скоростей. В начале на диаграмме перемещений проводятся хорды от начала отсчета до значений перемещений. Затем на диаграмме скоростей параллельно хордам проводятся прямые из полюса отстоящего от начала координат на расстояние Н=38,2 мм и до оси ординат.
Затем на пересечении полученных значений ординат и соответствующих углах мы получаем значения скоростной точки Е. Однако следует учесть, что углы смещаются влево на 150. Диаграмма перемещений показана на рисунке 10.
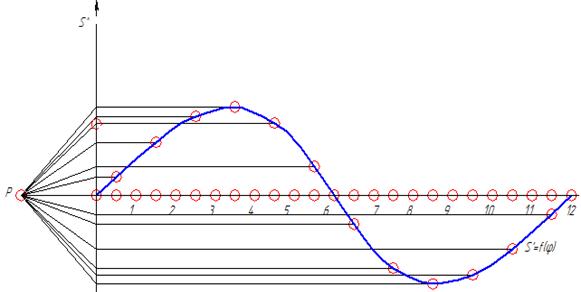
Рисунок 10 – Диаграмма аналогов скоростей
1.9 Построение диаграммы ускорений
Диаграмма ускорений строится аналогично диаграмме скоростей. Мы откладываем хорды на диаграмме скоростей, а затем откладываем отрезки на диаграмме ускорений на расстоянии Н от начала координат. На диаграмме ускорений углы смещаются вправо на 150. Диаграмма перемещений показана на рисунке 11.
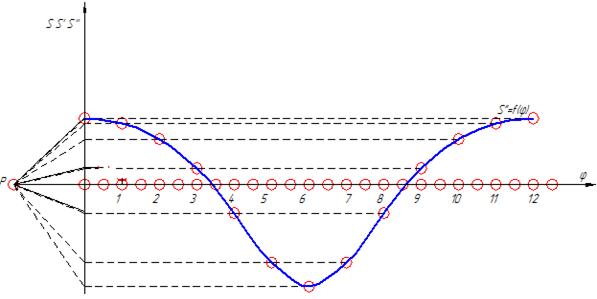
Рисунок 11– Диаграмма аналогов ускорений
