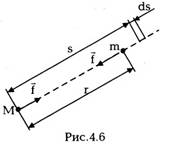
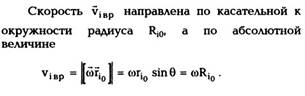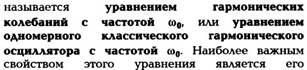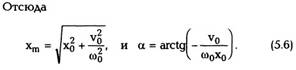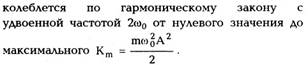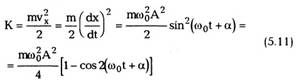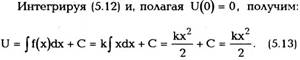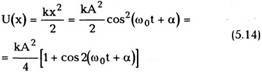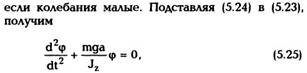совершает работу dA = fsds = fdr, то мощность
![]()
2. Теорема о кинетической энергии
|
ускорение частицы, получим |
|
|
|
Пусть частица массой m движется из точки 1 в
точку 2 по криволинейной траектории под
18
|
|
Сокращая на dt и преобразуя левую часть
Интегрируя теперь (4.8) от начальной точки 1
до конечной 2, получим окончательно:
![]()
где v{ — скорость тела в начале и v2 — в конце.
Выражение
![]()
называется кинетической энергией
материальной точки, а (4.9) — теоремой о кинетической энергии: приращение

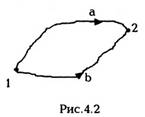
в точку 2 вдоль кривой а, а затем из точки 2 назад
в точку 1 вдоль кривой Ь. Общая работа, которая
производится при этом консервативной силой
![]()
т. е. работа не зависит от вида кривой,
соединяющей начальную и конечную точки 1 и 2.
Этот факт свидетельствует о том, что работа
консервативной силы является величиной,
имеющей глубокое физическое содержание.
4. Потенциальная энергия
Определим теперь важную характеристику
потенциального силового поля. Примем для этого
какую-либо точку в пространстве, которую
3. Потенциальные силы
Среди всех сил в природе существует целый
класс сил (не изменяющихся со временем),
обладающих следующим замечательным
свойством: если частица движется по замкнутому
пути, так что в результате движения она
возвращается в исходную точку, то работа,
совершаемая при этом силой, будет равна нулю.
Силы, обладающие таким свойством, называются
консервативными, или потенциальными. Если
сила f консервативна, то математически условие
потенциальности можно записать в следующем
виде:
![]()
где кружок означает, что интеграл вычисляется по
замкнутому пути L.
Кстати, интеграл типа (4.11) для произвольного
![]()
вектора А по замкнутому контуру L. Таким
образом, сила f потенциальна, если ее
циркуляция по любому замкнутому контуру равна
нулю.
Условие потенциальности можно
сформулировать другим способом: работа
консервативной силы при переносе частицы из
какой-то начальной точки 1 в конечную 2 не
зависит от вида пути, по которому происходит
перенос, а определяется только положением
начальной и конечной точек.
Действительно, рассмотрим две точки 1 и 2 и
соединим их двумя кривыми а и b (рис.4.2).
Предположим, что частица переводится из точки 1
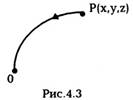
обозначим через О, за начало отсчета и будем
рассматривать работу консервативной силы при
переходе частицы из какой-либо произвольной
точки P(x, y,z) в точку О (рис.4.3). Величина этой
работы называется потенциальной энергией частицы. находящейся в точке Р, в потенциальном
силовом поле.
Она является функцией координат х, у, z
точки Р в неподвижной системе отсчета, т. е.
![]()
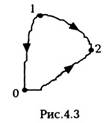
Работа консервативной силы? (рис.4.3) при
переходе частицы из точки 1 в точку 2 (работа не
зависит от пути!):
![]()
т. е. работа консервативной силы равна убыли
потенциальной энергии.
19
|
|
|
|
Это значит, что проекция силы на некоторое
направление s равна производной от U по
направлению s. Выражение (4.15) можно записать
в виде
![]()
откуда следует ( поскольку dU является полным
дифференциалом), что
![]()
лежит ниже нулевого уровня, z<0 и
потенциальная энергия отрицательна.
|
|
Пусть теперь имеются две частицы Мит,
которые притягиваются друг к другу силой
частицы m в точке Р, расположенной на
расстоянии г от М. Нулевой уровень выбираем на
бесконечном расстоянии от частицы М. Тогда
|
|
|
Тогда (4.17) принимают вид: |
Такие фундаментальные силы в природе, как
гравитационная и электрическая, являются силами
консервативными, для которых можно ввести
соответствующие потенциальные энергии. Так,
например, если частица m находится вблизи
поверхности Земли, то на нее действует
гравитационная сила тяжести mg, являющаяся
консервативной.
Выбираем точку О (начало отсчета
потенциальной энергии) на какой-то высоте над
поверхностью Земли и находим потенциальную
![]()
Такое же выражение мы получим, если
зафиксируем частицу m и будем перемещать на
бесконечность частицу М, поэтому потенциальная
энергия (4.21) называется потенциальной энергией гравитационного взаимодействия двух
частиц m и М. Она обращается в нуль, когда
частицы удалены друг от друга на бесконечно
большое расстояние. Эта же формула остается
справедливой, если частица m находится вне
однородного шара массой М (например, планеты).
В этом случае г — расстояние от частицы m до
центра шара.
Сила упругости пружины f = kx тоже
является консервативной. Нетрудно показать, что
потенциальная энергия деформированной
пружины
![]()
|
|
|
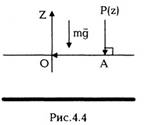
энергию частицы в произвольной точке P(z)
(рис.4.5) как работу постоянной силы mg,
направленной вертикально вниз, при
перемещении частицы из точки Р в точку О по
любому пути. Выбираем путь РАО. Тогда
![]()
так как АРА = mgz и ААО = 0 (здесь сила
перпендикулярна перемещению). Если точка Р
Причем нулевому уровню, как видно из (4.22),
соответствует состояние, когда пружина
недеформирована, т. е. когда х = 0.
5. Закон сохранения энергии
Вернемся теперь снова к теореме о
кинетической энергии (4.9). Пусть среди сил \ ,
действующих на частицу т, часть сил является
20
|
|
|
|
|
|
|
|
Следует помнить при решении конкретных
задач, что типичными неконсервативными силами
являются силы трения и силы сопротивления. Из
(4.23) следует закон сохранения энергии для
материальной точки: полная энергия частицы не
изменяется,__ если__ на__ нее__ действуют__ только
консервативные силы.
Рассмотрим теперь систему из п
взаимодействующих между собой материальных
точек. Полная механическая энергия системы Е
складывается теперь из кинетической энергии
системы
![]()
|
Потенциальная энергия взаимодействия частиц |
|
потенциальной энергии взаимодействия UR3
частиц системы, которая определяется их
консервативными силами взаимодействия, и
потенциальных энергий частиц в поле всех
находится их энергия взаимодействия U^ подобно
|
Итак, полная механическая энергия системы |
|
тому, как это делалось при выводе формулы (4.21)
для энергии взаимодействия двух масс,
притягивающихся согласно закону всемирного
тяготения. После этого
неконсервативных, как внутренних, так и
внешних сил. Если таких сил нет, полная энергия
Е (4.27) системы не изменяется со временем
(закон сохранения энергии для системы).
Используем теперь полученные соотношения
(4.25) — (4.27) для абсолютно твердого тела,
рассматривая его как совокупность жестко
связанных материальных точек. Полную энергию
тела на основании (4.27) можно записать в
|
|
|
|
|
|
|
следующем виде (полагая UB3 частиц тела равной
нулю):
21
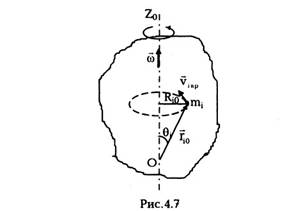
Следует отметить, что при плоском движении
и скорость vt, и viBp находятся в плоскости XOY
неподвижной системы координат,
перпендикулярной оси вращения OZ. Для
нахождения кинетической энергии тела
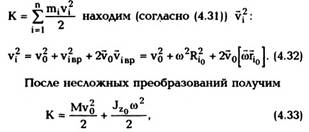
![]()
момент инерции тела относительно оси вращения OZqi проходящей через центр масс тела.
|
|
Итак, при плоском движении твердого тела его
полная энергия
22
Лекция 5. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
Одномерный гармонический осциллятор; энергия гармонического осциллятора;
математический маятник; физический маятник.

|
1. Одномерный гармонический
осциллятор.
Колебания являются широко
распространенным видом движения и
наблюдаются в системах самой разнообразной
природы. Колебания относятся к процессам, точно
повторяющимся через одинаковый промежуток
времени То, который называется периодом колебаний. При механических колебаниях,
например, повторяются положения тел в
пространстве и их скорости. Электрические
колебания — это повторяющиеся изменения
напряжений и сил токов в электрических цепях.
Однако, несмотря на разную физическую
природу, в колебаниях проявляются одни и те же
закономерности, которые исследуются общими
методами.
Важной кинематической характеристикой
является форма колебаний. Она определятся
видом той функции времени t, которая описывает
изменение той или иной физической величины
при колебаниях. Наиболее важными (и наиболее
простыми) являются так называемые
гармонические колебания. Они описываются
гармоническим законом
![]()
Здесь x(t) характеризует изменение какой— либо
физической величины при колебаниях, например,
x(t) может быть смещением маятника от
положения равновесия, мгновенным значением
заряда на конденсаторе в электрическом
колебательном контуре или плотностью воздуха в
звуковой волне.
|
|
Система, закон движения которой имеет вид
(5.1) называется одномерным классическим
гармоническим осциллятором. Циклическая
частота со0 связана с периодом колебаний по
формуле:
![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
Полученное дифференциальное уравнение для
x(t)
23
|
|
|
свойству: колебания могут возникнуть в любой
системе, обладающей положением устойчивого равновесия. При выводе системы из равновесия
она начнет колебаться около положения
равновесия (не обязательно, конечно, по
гармоническому закону!). Для механической
системы в положении равновесия сумма сил,

|
|
Рассмотрим одномерное (вдоль оси х)
движение материальной точки массой т,
обладающей положением устойчивого равновесия,
куда мы поместим начало координат х = 0. При
смещении частицы вправо на х на частицу
начинает действовать сила fx = - f(x),
направленная к началу координат. Эта сила
называется возвращающей силой. Запишем
второй закон Ньютона (в проекции на ось х) для
нашей частицы:
Сравнивая полученное уравнение (5.7) с
уравнением гармонических колебаний (5.3), мы
видим, что материальная точка будет колебаться
около положения равновесия по гармоническому
закону (5.1) только в том случае, если
возвращающая сила линейно зависит от х:
f(x) = kx. (5.8)
где коэффициент пропорциональности к, который
определяется свойствами конкретной системы,
называется коэффициентом возвращающей силы. При этом частота колебаний
![]()
2. Энергия гармонического
осциллятора.
|
|
|
|
|
|
|
|
Полная энергия одномерного гармонического
осциллятора
|
|
|
|
Если между f (х) их нет линейной зависимости,
колебания не будут гармоническими. Такие
колебания называются ангармоническими. Для
таких колебаний принцип суперпозиции не
выполняется, и мы не будем их рассматривать.
Особая важность гармонических колебаний
связана, как можно доказать, с тем, что любая
система будет колебаться по гармоническому
закону, если ее вывести из положения
устойчивого равновесия на очень маленькую
величину. Такие гармонические колебания
называются малыми.
Таким образом, мы показали, что частота и
период гармонического осциллятора не зависят от
начальных условий, а определяются только
свойствами конкретной механической системы —
ее массой и коэффициентом возвращающей силы
к.
|
Сравнивая (5.21) с (5.13), находим
коэффициент возвращающей силы
математического маятника при малых колебаниях:
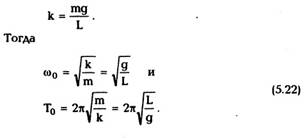
4. Физический маятник.
Его образует твердое тело, подвешенное в поле
тяжести на закрепленной горизонтальной оси,
которую примем за ось OZ (см. рис. 5.2).
|
|
|
|
то есть средние значения кинетической и
потенциальной_____ энергии____ гармонического
осциллятора равны друг другу и каждое из них
составляет половину полной энергии. Этот вывод
используется в молекулярной физике.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 |