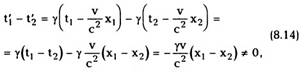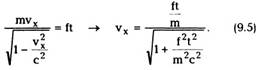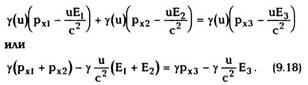Это важное соотношение, связывающее
частоту со с волновым числом к, характерно для
природы волны и называется дисперсионным уравнением.
Вместо того, чтобы писать в левой части (7.11)
сумму вторых частных производных по
координатам, мы можем представить ее так:
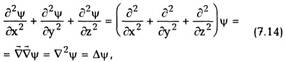
32
|
|
4. Дисперсия
Обратимся теперь к рассмотрению обеих
скоростей волн — фазовой и групповой — и
сравним их между собой. Из определения
фазовой скорости (7.19) следует, что
скоростью волн. Для того, чтобы ее отыскать,
напишем условие постоянства фазы волны:
![]()
Тогда групповая скорость (см. (7.20))
![]()
|
|
откуда фазовая скорость
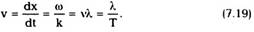
Найдем теперь отдельно скорость
перемещения определенной амплитуды волны
Очевидно, что эта скорость совпадает со
скоростью перемещения группы в целом; она
называется поэтому групповой скоростью. Для
отыскания ее пишем, по аналогии с предыдущим,
условие постоянства амплитуды:
![]()
Если фазовая скорость v, образующих пакет
гармонических волн, не зависит от к (или X), то
говорят, что среда, в которой распространяется
волна, не обладает дисперсией. В этом случае
|
|
|
|
|
|
|
|
Отсюда находим |
и будем называть групповой скоростью: |
Мы видим, таким образом, что обе эти
скорости: фазовая и групповая, выражаются
различными формулами. Чтобы разобраться в
соотношении между ними, нужно рассмотреть
условия распространения волн в различных
средах.
|
|
Можно показать, что путем суперпозиции
плоских волн можно осуществить волновой
процесс, в котором амплитуда отлична от нуля
только в небольшой части пространства Δх, а в
остальном пространстве равна нулю. Для этого
нужно, чтобы волновые числа плоских волн
лежали в некотором интервале Δк, причем
Соотношение (7.21), как мы узнаем позже,
приводит к знаменитым соотношениям неопределенностей Гейзенберга в квантовой
механике.
|
При наличии же дисперсии групповая скорость
не совпадает с фазовой, а именно, в зависимости
от знака производной dv/dk групповая скорость
говорят, что среда обладает нормальной дисперсией, а во втором — аномальной. В оптике
осуществляются оба эти случая. Так, в вакууме
Возникает вопрос: какая же из этих скоростей
измеряется на опыте при определении, например,
скорости света. Анализ различных методов
измерения скорости света показывает, что ни
один из них не дает возможности определить
фазовую скорость, но все они дают групповую
скорость.
Из сказанного следует, что фазовая скорость в
точном соответствии со своим названием дает
лишь скорость перемещения определенной фазы
и, как показывает более строгий анализ,
совершенно не связана, например, со скоростью
движения фронта ограниченного в пространстве
пакета волн (сигнала) или со скоростью движения
энергии волны, которые определяются как раз
групповой скоростью.
Именно поэтому возникновение фазовой
скорости, большей скорости света в пустоте с, ни
в коем случае не противоречит утверждению
теории относительности (см. следующую лекцию)
о том, что скорость света в пустоте есть
предельная скорость.
В частности, в оптике доказывается, что
скорость фронта волны при любых условиях
равна с, т. е. скорости света в пустоте.
33
Лекция 8. КИНЕМАТИКА СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ (СТО)
Постулаты СТО; преобразования Лоренца; следствия из преобразований
Лоренца.
 1. Постулаты СТО.
1. Постулаты СТО.
Как уже говорилось в лекции 1, законы
ньютоновской (классической) механики
становятся неприменимыми при изучении
движения частиц, скорости v которых сравнимы
со скоростью света в пустоте с =3 108 м/с. В этом
случае следует использовать законы так
называемой специальной теории
относительности (СТО), созданной
А. Эйнштейном в 1905 году. В основе СТО лежат
два постулата.
1. Постулат относительности.
Все явления природы (механические,
электромагнитные, оптические и т. д.) протекают
одинаково во всех инерциальных системах
отсчета (ИСО), то есть все законы природы
выглядят одинаково во всех инерциальных
системах отсчета. Данный постулат является
обобщением принципа относительности Галилея,
относящегося только к механическим явлениям,
на все явления природы.
2. Постулат постоянства скорости света.
Скорость света в пустоте одинакова во всех
системах отсчета, независимо от относительного
движения источника света и наблюдателя. Следует
отметить, что этот постулат подтвержден
многочисленными тонкими экспериментами.
В классической механике для перехода от
одной ИСО к другой, движущейся равномерно
относительно первой, используются так
называемые преобразования Галилея.
Рассмотрим две декартовы прямоугольные
системы координат K(x, y,z) и K'(x',y',z') (рис.
8.1). Пусть их оси ОХ и ОХ' совпадают и
положим, что система К' равномерно движется со
какой —либо точки Р в К и К' связаны
соотношениями:

К этим трем соотношениям следует добавить
еще соотношение для времени: время в обеих
системах с точки зрения классической механики
топот плиняклип тп с*сти
![]()
Формулы (8.1) и (8.2) представляют собой
имеющие место в ньютоновской механике так
называемые преобразования Галилея. Легко
убедиться, что уравнения ньютоновской механики
не изменяют своего вида при замене координат и
времени согласно этим формулам, или, как
говорят, уравнения механики Ньютона
инвариантны относительно преобразований
Галилея, то есть законы механики Ньютона
выглядят одинаково во всех ИСО.
В самом деле, напишем второй закон Ньютона
для частицы m в проекции на ось ОХ' системы К':
![]()
Дифференцируем первое соотношение (8.1) по
времени t':
![]()
или
![]()
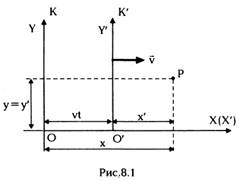
скоростью v относительно К вдоль оси ОХ,
причем в момент t = 0 их начала координат О и О'
совпадают. Совершенно очевидно, что координаты
Это известная теорема сложения скоростей в
механике Ньютона.
Дифференцируя (8.4) второй раз, получим
![]()
Итак, левые части ньютоновских уравнений не
меняются при преобразованиях Галилея. В правых
же частях этих уравнений стоят компоненты
силы, зависящие только от расстояний которые не
меняются при использовании преобразований
Галилея.
Действительно, расстояние между любыми
двумя точками A(x',y',z') и B(x',y',z')
34
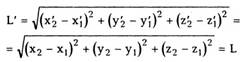
|
Подставляя (8.5) и (8.6) в (8.3), получим: |
|
одинаково во всех ИСО, если использовать
преобразования Галилея. Поэтому эти
преобразования не меняют компонентов сил, то
есть
то есть преобразования Галилея не меняют
ньютоновских уравнений движения, или, как
говорят, эти уравнения инвариантны относительно
преобразований Галилея, что является
математической формулировкой принципа относительности Галилея: законы механики
выглядят одинаково во всех ИСО.
Первый постулат СТО согласуется с этим
принципом и обобщает принцип относительности
на другие явления, в частности, на законы
распространения света. Однако одновременное
применение обоих постулатов СТО находится в
противоречии с преобразованиями Галилея. В
самом деле, если применить теорему сложения
скоростей (8.4) к свету, то получается, что, если
скорость света в системе К равна с, то в системе
К' она должна быть равна с' = с —v, что
противоречит второму постулату СТО.
Так как, однако, оба эти постулата
подтверждаются всеми известными
экспериментальными фактами, то противоречие
имеется не между постулатами, а между
постулатами и преобразованиями Галилея: эти
преобразования неприменимы к распространению
света и к движениям со скоростями, близкими к
скорости света, то есть "очевидные"
преобразования Галилея следует заменить
новыми, но такими, чтобы они переходили в
преобразования Галилея при движениях со
скоростями v « с.
2. Преобразования Лоренца.
Эйнштейну удалось получить такие
преобразования, но для этого ему пришлось
отказаться от привычных представлений о
пространстве и времени. Так, согласно
Эйнштейну, время не является абсолютным
понятием, а течет по разному в разных ИСО (tVt).
Эти преобразования имеют следующий вид:
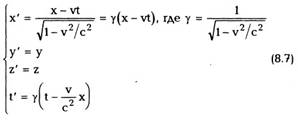
![]()
условиях, когда верна механика Ньютона,
преобразования (8.3) автоматически переходят в
преобразования Галилея (8.1) Выразим теперь из
(8.7) x, y,z, t через x',y',z',t' (обратные
преобразования). Получаем:
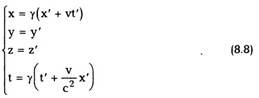
Преобразования (8.7) и (8.8) называются
преобразованиями Лоренца, который нашел их
ранее, но чисто формальным путем. Дело в том,
что до создания СТО английским физиком
Д. Максвеллом была написана система уравнений,
описывающая электромагнитные и оптические
явления (уравнения Максвелла). Из этих
уравнений следовало, что свет в пустоте должен
распространяться со скоростью с в любой ИСО,
однако сами уравнения Максвелла оказались не
инвариантными относительно преобразований
Галилея. Лоренц же чисто формальным путем
нашел преобразования, относительно которых
уравнения Максвелла оказываются
инвариантными.
|
Произведем теперь переход от системы К к |
|
|
Мы не будем выводить преобразования
Лоренца, но для оправдания покажем, что именно
они обеспечивают отсутствие противоречия
между обоими постулатами СТО. Рассмотрим для
этого снова две ИСО К и К'. Предположим, что в
момент t = 0, когда начала О и О' систем К и К'
совпадают, в точке О (и О') происходит вспышка
света. Через время t свет распространяется в
системе К на расстояние ct и достигает
сферической поверхности с радиусом R = ct,
уравнение которой имеет вид
то есть снова получаем уравнение сферической
поверхности, но с центром в О'. Мы видим, что
благодаря преобразованиям Лоренца и
постоянству скорости света удовлетворяется и
первый постулат относительности: волна,
выходящая из общего начала координат при t = 0,
остается сферической как в системе К, так и в
системе К' относительно О'. На первый взгляд
кажется непонятным, каким образом
геометрическое место точек (сфера с центром в
О'), которых достигает свет в системе К', остается
сферой с центром в О в системе К. Этот
35
кажущийся парадокс связан с тем, что события,
одновременные в одной системе отсчета, не будут
одновременными в другой.
Найдем теперь, используя преобразования
Лоренца, теорему сложения скоростей в СТО. Берем дифференциал соотношений (8.7):
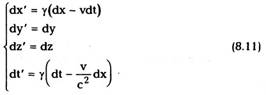
Деля первые три равенства на четвертое,
получим:
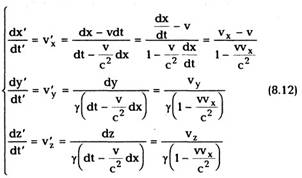
При v/c « 1 эти преобразования переходят в
теорему сложения скоростей Галилея.
Обратные преобразования получаются из (8.12)
простым изменением знака перед v, то есть
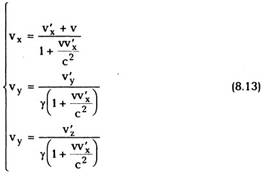
3. Следствия из преобразований
Лоренца.
а) Относительность одновременности.
|
|
В классической физике считалось, что два
события, которые произошли одновременно в
одной ИСО, будут одновременными и в другой
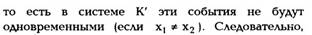
понятие одновременности в СТО является
понятием относительным.
б) Сокращение длины.
Имеется стержень, длина которого, измеренная
в той ИСО, где он покоится, равна Lq. Эта длина
называется собственной длиной. Пусть стержень
покоится в системе К' и расположен вдоль оси у'
или z', тогда его собственная длина
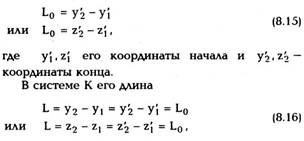
|
В системе К длина движущегося со скоростью |
|
то есть поперечные движению стержня размеры
остаются неизменными. Если же стержень
расположен вдоль оси х' в системе К', то его
собственная длина
причем координаты х, и х 2 необходимо измерить
одновременно по часам в системе К (то есть при
ti=t2).
Подставляя преобразования Лоренца (8.7) в
(8.17), получим
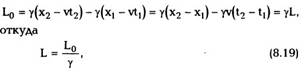
то есть продольные размеры движущегося
стержня сокращаются в у раз. Нетрудно показать,
что стержень, покоящийся в системе К, тоже
сокращается в у раз с точки зрения наблюдателя,
находящегося в системе К'.
в) Замедление хода времени.
|
|
Промежуток времени между этими же |
Промежуток времени между двумя
последовательными событиями, происшедшими в
одной точке пространства и измеренный по
неподвижным часам, расположенным в этой
точке, называется собственным промежутком
36
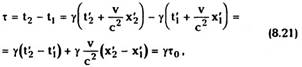
то есть с точки зрения наблюдателя в системе К
движущиеся часы (те, что покоятся в системе К')
идут в у раз медленней. Опять же нетрудно
показать, что с точки зрения наблюдателя в
системе К' идут медленнее те часы, которые
покоятся в системе К.
Рассмотрим в заключение некоторые примеры
сложения скоростей в СТО.
Пусть в системе К' движется частица вдоль
оси х' со скоростью v'x = 0.9с, а сама система К'
движется относительно К со скоростью v = 0.9с.
Какова скорость этой частицы в системе К?
Согласно преобразований Галилея скорость
частицы vx = v'x + v = 1.8с > с. Из преобразований
Лоренца (8.13)
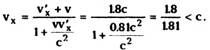
Пусть теперь в системе К' движется вдоль х'
свет со скоростью v'x = с. Его скорость в системе
![]()
постулатом СТО, согласно которому скорость
света одинакова во всех инерциальных системах
отсчета.
37
Лекция 9. ДИНАМИКА СТО
Второй закон Ньютона в СТО; энергия свободной частицы; связь энергии и
импульса; эквивалентность энергии и массы.
 |
|
|
|
|
|
|
|
|
|
1. Второй закон Ньютона в СТО.
Перейдем теперь к рассмотрению динамики
материальной точки (частицы) в теории
относительности.
Прежде всего заметим, что закон инерции
(первый закон Ньютона) является инвариантным
относительно преобразований Лоренца.
Действительно, если в некоторой ИСО К частица
движется с постоянной скоростью, то и в любой
другой системе К' скорость частицы согласно
преобразований Лоренца останется постоянной.
Второй же закон Ньютона, как мы знаем,
инвариантен относительно преобразований
Галилея, поэтому, согласно Эйнштейну, его
следуем так изменить, чтобы он стал
инвариантным относительно преобразований
Лоренца.
|
но изменить ньютоновское определение импульса |
|
|
Оказывается, этого можно добиться, если
записать второй закон Ньютона через импульс
частицы р в классической форме (см. лекцию 2,
соотношение (2.8))
Следует отметить, что при выводе выражения
(9.2) исходили из требования выполнения закона
сохранения импульса для системы релятивистских
частиц.
|
|
Если частица движется со скоростью v<<c,
соотношение (9.2) переходит в классическое.
покоилась в начале координат при t = 0, начала
действовать постоянная сила f = [f, 0,0} ,
направленная вдоль оси ОХ. Найти скорость
частицы в зависимости от времени t.
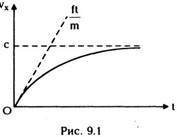
|
|
Посмотрим, как ведет себя частица в СТО. Из |
Классическая частица будет двигаться
38
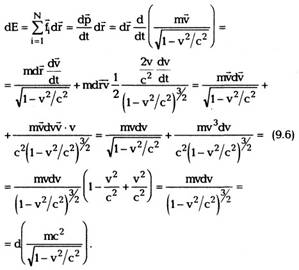
|
|
Исходя из (9.6), определим энергию свободной
частицы как
Дело в том, что при выборе const = - me2
преобразование Лоренца для скорости не
переходило бы в формулу сложения скоростей в
классической механике.
3. Связь энергии и импульса.
Обсудим теперь некоторые следствия из
полученных формул. Во первых, из определения
импульса (9.2) и энергии частицы (9.7) следует, что
импульс частицы связан с ее энергией
соотношением
![]()
Из этой формулы следует, в частности, что,
если какая —либо частица может двигаться со
скоростью v = c, то ее импульс связан с энергией
по формуле
![]()
Далее, возводя (9.2) в квадрат и вычитая из
полученного выражения Е2/с2 , получим
|
|
|
![]()
Второе слагаемое в (9.8) совпадает с
кинетической энергией частицы в классической
механике. Однако, при v = 0 энергия свободной
частицы (энергия покоя)
![]()
оказывается отличной от нуля. Таким образом,
СТО приводит к новому, весьма важному выводу:
всякая частица или тело, обладающее массой т.
обладает вместе с тем энергией покоя тс2.
Естественно тогда определить кинетическую
энергию частицы в СТО, как
![]()
|
|
Это выражение переходит в классическое,
если скорость частицы v « с. На первый взгляд
может показаться, что определение энергии (9.7)
является произвольным. Поскольку энергия
найдена из дифференциального соотношения (9.6),
ее можно определить как
таким образом энергия при v«с будет
совпадать с кинетической энергией частицы в
классической механике. В действительности,
однако, легко показать, что константу следует
положить равной нулю, как это было сделано в
(9.7).
лекции), инвариантной относительно
преобразований Лоренца, так как справа в (9.12)
стоит масса частицы, одинаковая во всех ИСО.
Отсюда следует, что при переходе от системы К к
системе К' (или наоборот) компоненты импульса
![]()
x, y,z и t. Делая в (8.7) соответствующие замены,
получим:
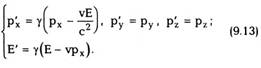
4. Эквивалентность массы и энергии
Рассмотрим теперь неупрутое столкновение
двух частиц. Предположим, что две одинаковые
частицы массой m движутся в системе К
навстречу друг другу вдоль оси ОХ с одинаковыми
скоростями v. Тогда
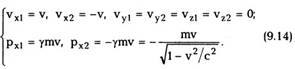
После столкновения они слипаются, образуя
новую частицу. Так как до столкновения
![]()
39
|
новая частица после столкновения покоится
то есть масса новой частицы М превысила
исходную массу 2т на
|
В другой системе К', движущейся
относительно К со скоростью и :
|
|
Подставляя (9.13) в (9.17), получим
так как кинетическая энергия превратилась в
массу. Изменение массы AM, связанное с
превращением кинетической энергии в массу, в
повседневных процессах обычно очень мало и не
поддается измерениям.
имеющих |
Так, при столкновении и слипании двух
|
шариков массой
добавочная |
одинаковые по величине и противоположные по
|
направлению скорости
масса
|
С учетом (9.15), (9.16) имеем |
Этот результат свидетельствует о том, что в
СТО, в отличие от ньютоновской механики,
энергия при неупругом столкновении сохраняется.
|
Поскольку
частица покоится, то есть Е3 — ее энергия покоя,
мы вынуждены на основании (9.19) утверждать,
что масса образовавшейся частицы М>2т, так как
из (9.19) следует, что
![]()
|
Мы получили новый важный результат: в СТО,
в отличие от механики Ньютона, нет закона сохранения массы системы частиц - она может
возрастать или уменьшаться, в зависимости от
того, какие превращения происходят с
кинетической энергией входящих в систему
частиц. В данном примере кинетическая энергия
после |
исходных частиц
![]()
Эта величина значительно меньше ошибки, с
которой может быть измерена масса в 1г.
Совсем другая ситуация наблюдается в
процессах, происходящих внутри атомного ядра,
состоящего из элементарных частиц протонов и
нейтронов, массы которых хорошо известны:
![]()
|
|
частицы удерживаются так называемыми
ядерными силами. Так, ядро тяжелого водорода
(дейтерия) состоит из одного протона и одного
Откуда взялась эта разница? Дело в том, что
для разделения ядра дейтерия на протон и
нейтрон необходимо затратить энергию, чтобы
преодолеть мощные ядерные силы,
удерживающие эти частицы в ядре. Эта энергия
называется энергией связи ядра. Для ядра
дейтерия экспериментально измеренная энергия
связи Есв = 2,226 МэВ. Разделяя ядро дейтерия, мы
увеличиваем массу ядра на величину
столкновения обратилась в нуль, то есть
изменилась на
![]()
или, на основании (9.20),
![]()
![]()
что совпадает с (9.22).
Взаимное превращение энергии и массы
играет фундаментальную роль в ядерных
реакциях деления и синтеза. Так, например,
важнейшим источником энергии Солнца и
большинства звезд является ядерное "сжигание"
протонов с образованием ядер гелия.
40
Лекция 10. ВВЕДЕНИЕ В МОЛЕКУЛЯРНО-КИНЕТИЧЕСКУЮ ТЕОРИЮ
Количество вещества; абсолютная температура, макроскопические
параметры; основное уравнение кинетической теории идеального газа,
уравнение состояния идеального газа.

|
Число молекул в одном моле получается |
1. Количество вещества
Любое вещество (газообразное, жидкое или
твердое) состоит из огромного числа мельчайших
частиц, сохраняющих все химические свойства
данного вещества. Эти мельчайшие частицы
называются молекулами. Сами молекулы могут
состоять из нескольких более простых частиц —
атомов.
Если различных видов молекул известно
огромное число (миллионы), то различных атомов
всего 105, причем в природе их встречается 88, а
17 получены искусственным путем. Это атомы так
называемых химических элементов. Размеры
молекул и атомов чрезвычайно малы, порядка
|
велико. В одном |
Зато число их в веществе необычайно
грамме воды, например,
содержится примерно
![]()
|
Согласно современным измерениям |
|
Массы атомов и молекул тоже малы, поэтому
их удобней измерять не в килограммах, а в
специальных единицах. Эта единица называется
атомной единицей массы (а. е.м.). По
определению
Масса атома, выраженная в а. е.м., называется
относительной атомной массой А и приведена в
таблице Менделеева. Масса молекулы,
выраженная в а. е.м., называется относительной молекулярной массой |i' и равна, очевидно, сумме
относительных масс атомов, составляющих
данную молекулу. Для нахождения массы
молекулы в килограммах m нужно ее
относительную молекулярную массу ц' умножить
на то, то есть
![]()
В молекулярной физике широко используется
понятие количества вещества. Единица
количества вещества называется молем. По
определению моль вещества — это такое
количество вещества, масса которого в
килограммах численно равна 10~3ц\ где ц' —
относительная молекулярная масса данного
вещества. Масса одного моля ц называется
молярной массой вещества, причем
![]()
Следовательно, в моле любого вещества
содержится одинаковое число молекул (при
получении (10.5) ц' сократилась!), равное 6,02-1023.
Это число называется числом Авогадро NA.
|
|
Если тело обладает массой М, то оно содержит
молекул.
2. Абсолютная температура. Макроскопические параметры
Между молекулами вещества существуют силы
взаимодействия: на больших расстояниях друг от
друга молекулы притягиваются, а при сближении
они отталкиваются. На это указывает сам факт
существования различных агрегатных состояний
вещества. В твердом и жидком состояниях
молекулы притягиваются друг к другу настолько,
что тела сохраняют свой объем, а в случае
твердого тела — еще и форму. В газообразном же
состоянии силы взаимодействия значительно
меньше, так что газ заполняет весь
предоставленный ему какой угодно объем.
Последний факт указывает еще на одну
характерную особенность частиц любого
вещества: молекулы вещества находятся всегда в
постоянном движении. Отличительной чертой
этих движений является их полная
беспорядочность, хаотичность. Это хаотическое
движение молекул носит название теплового движения. В твердых телах тепловое движение
состоит из беспорядочных колебаний молекул
около своих положений равновесия, образующих
правильную кристаллическую решетку. Именно в
хаотическом тепловом движении молекул
заключена природа теплоты и тепловых явлений.
Если привести в соприкосновение два тела, то
их молекулы в месте контакта будут передавать
друг другу энергию. Тело, которое при этом
теряет энергию, называют более нагретым, а тело,
к которому энергия переходит, — менее
нагретым. Как показывает опыт, такой переход
41
|
|
движения, приходящаяся на одну степень |
В технике и быту часто используется не шкала |
энергии продолжается до тех пор, пока не
установится определенное состояние — состояние
теплового равновесия. Время т, в течение
которого устанавливается равновесие, называется
временем релаксации.
Для характеристики степени нагретости тел в
состоянии равновесия служит понятие
температуры. В физике в качестве температурной
шкалы пользуются так называемой абсолютной шкалой, имеющей глубокий физический смысл.
Дело в том, что физическое определение
температуры должно основываться не на
случайной величине, а на величине, которая
выравнивается для двух любых тел, приходящих в
состояние теплового равновесия друг с другом.
Оказывается, что таким замечательным свойством
обладает средняя кинетическая энергия поступательного движения частиц (молекул или
![]()
выбрана в качестве мерила температуры, где m —
масса молекулы, v0 — скорость ее центра масс и
значок ( ) означает усреднение по всем
молекулам, движущимися с разными скоростями.
|
|
По определению абсолютная температура Т в
Кельвинах
переводящий температуру в Джоулях в Кельвины,
называется постоянной Больцмана.
Из (10.7) следует, что в состоянии теплового
равновесия при температуре Т средняя
кинетическая энергия поступательного движения
молекулы
![]()
Следует отметить, что эта формула
справедлива не только для молекул вещества, но и
для частиц больших, макроскопических размеров,
например, мелких пылинок, взвешенных в
жидкости, которые можно наблюдать через
микроскоп (так называемое броуновское
движение).
|
|
Поскольку любая молекула обладает тремя
поступательными степенями свободы (три
координаты х0, у0, z0 ее центра масс) и все они
равноправны
поступательного движения, приходящаяся на одну
(i-ую) степень свободы. Сравнивая (10.9) с (10.8),
заключаем, что в состоянии теплового равновесия
средняя кинетическая энергия поступательного
Поскольку кинетическая энергия молекулы
является положительной величиной, абсолютная
температура Т — величина положительная и
стремится к нулю, когда хаотическое тепловое
движение молекул прекращается (по шкале
Цельсия это происходит при t = —273,15°).
Благодаря тепловому движению молекул, газ
(или жидкость) оказывает давление на стенки
заключающего его сосуда. Молекулы вещества,
сталкиваясь со стенкой, передают ей часть своего
импульса. Изменение же импульса стенки в
единицу времени (вспомним механику!)
определяет действующую на нее силу. Отношение
проекции силы Afn на нормаль к площадке на
стенке AS называется давлением газа (или
жидкости) на этом участке:
![]()
Свойства тел, рассматриваемых в целом, не
вдаваясь в детали их молекулярной структуры (с
которой эти свойства в действительности жестко
связаны) называются макроскопическими параметрами тела. К числу этих параметров
относится температура тела Т, давление Р и объем
тела V.
Однако, как оказывается, эти три параметра не
являются независимыми. Уравнение f(Т, Р, V) = 0,
связывающее эти три величины, называется
уравнением состояния данного тела и является
одним из важнейших соотношений,
характеризующих его тепловые свойства.
Получить же теоретически уравнение состояния
удается лишь в случае самых простых тел
(например, для идеального газа).
Следует теперь уточнить введенное ранее
понятие теплового равновесия, как состояния, в
котором температуры двух соприкасающихся тел
выравниваются. Вообще, состоянием теплового равновесия системы тел называется такое
состояние, при котором не происходит никаких
самопроизвольных тепловых процессов и все
части системы покоятся друг относительно друга,
не совершая никаких макроскопических
движений. Отсюда следует, что в состоянии
равновесия выравниваются не только
температуры составляющих систему частей, но и
их давления, иначе эти части пришли бы в
движение.

|
Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 |